Omega-categorical theory
In mathematical logic, an omega-categorical theory is a theory that has only one countable model up to isomorphism. Omega-categoricity is the special case κ =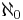 
= ω of κ-categoricity, and omega-categorical theories are also referred to as ω-categorical. The notion is most important for countable first-order theories.
Equivalent conditions for omega-categoricity
Many conditions on a theory are equivalent to the property of omega-categoricity. In 1959 Erwin Engeler, Czesław Ryll-Nardzewski and Lars Svenonius, proved several independently[1]. Despite this, the literature still widely refers to the Ryll-Nardzewski theorem as a name for these conditions. The conditions included with the theorem vary between authors[2][3].
Given a countable complete first-order theory T with infinite models, the following are equivalent:
- The theory T is omega-categorical.
- Every countable model of T has an oligomorphic automorphism group.
- Some countable model of T has an oligomorphic automorphism group.
- The theory T has a model which, for every natural number n, realizes only finitely many n-types, that is, the Stone space Sn(T) is finite.
- For every natural number n, T has only finitely many n-types.
- For every natural number n, every n-type is isolated.
- For every natural number n, up to equivalence modulo T there are only finitely many formulas with n free variables, in other words, every nth Lindenbaum-Tarski algebra of T is finite.
- Every model of T is atomic.
- Every countable model of T is atomic.
- The theory T has a countable atomic and saturated model.
- The theory T has a saturated prime model.
Notes
- ^ Rami Grossberg, José Iovino and Olivier Lessmann, A primer of simple theories
- ^ Hodges, Model Theory, p. 341.
- ^ Rothmaler, p. 200.
References
- Chang, Chen Chung; Keisler, H. Jerome (1989) [1973], Model Theory, Elsevier, ISBN 978-0-7204-0692-4
- Hodges, Wilfrid (1993), Model theory, Cambridge: Cambridge University Press, ISBN 978-0-521-30442-9
- Hodges, Wilfrid (1997), A shorter model theory, Cambridge: Cambridge University Press, ISBN 978-0-521-58713-6
- Poizat, Bruno (2000), A Course in Model Theory: An Introduction to Contemporary Mathematical Logic, Berlin, New York: Springer-Verlag, ISBN 978-0-387-98655-5
- Rothmaler, Philipp (2000), Introduction to Model Theory, New York: Taylor & Francis Group, ISBN 978-90-5699-313-9